Sitemize üye olarak beğendiğiniz içerikleri favorilerinize ekleyebilir, kendi ürettiğiniz ya da internet üzerinde beğendiğiniz içerikleri sitemizin ziyaretçilerine içerik gönder seçeneği ile sunabilirsiniz.
Sitemize üye olarak beğendiğiniz içerikleri favorilerinize ekleyebilir, kendi ürettiğiniz ya da internet üzerinde beğendiğiniz içerikleri sitemizin ziyaretçilerine içerik gönder seçeneği ile sunabilirsiniz.
Üyelerimize Özel Tüm Opsiyonlardan Kayıt Olarak Faydalanabilirsiniz

Sıradaki içerik:
Yazılım Mühendisliği : Detaylı ve Teknik Bir Bakış
Sayı Kümeleri: Bilimsel ve Detaylı Bir Bakış
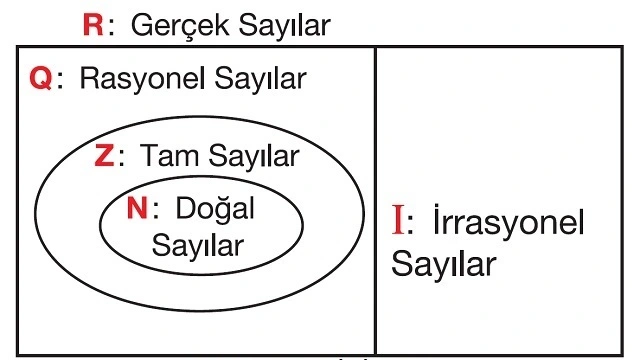
Sayı kümeleri, matematiksel kavramların çoğu için temel oluşturan önemli bir konudur. Bu kümeler, sayıları belirli özelliklerine göre gruplandıran, matematiksel düşünme ve analiz yapısına çok önemli bir çerçeve sunan büyük bir sistemdir. Bu yazıda, doğal sayılar, tam sayılar, rasyonel sayılar, irrasyonel sayılar, reel sayılar ve karmaşık sayılar gibi farklı sayı kümelerini detaylı bir şekilde inceleyeceğiz.
1. Doğal Sayılar (ℕ)
İçindekiler
ToggleDoğal sayılar, en temel sayı kümesi olarak kabul edilir. Doğal sayılar, 0, 1, 2, 3, 4, … gibi pozitif tam sayılardan oluşur. Bu küme, sayma işleminde kullanılan ilk sayıları kapsar ve çoğu zaman çocukluk döneminde matematiğin temeli olarak öğretilir.
Doğal sayılar kümesi, sonsuz bir kümedir ve her doğal sayıdan sonra başka bir doğal sayı gelir. Bu durum, doğal sayıların aritmetiksel işlemler ve sıralama işlemlerinde kullanımını sağlar. Bu küme, genellikle ℕ sembolüyle gösterilir.
2. Tam Sayılar (ℤ)
Tam sayılar, doğal sayıları, bunların negatiflerini ve sıfırı kapsayan bir kümedir. Yani, tam sayılar, … -3, -2, -1, 0, 1, 2, 3, … şeklindedir. Bu küme, pozitif ve negatif sayıların birleşiminden oluştuğu için hem çıkarma hem de toplama işlemleri açısından daha geniş bir küme sunar.
Tam sayılar, sıfır etrafında simetrik bir yapıya sahiptir ve bu durum, negatif sayılarla işlem yapma ihtiyacının karşılanmasını sağlar. Tam sayılar kümesi genellikle ℤ sembolü ile ifade edilir.
3. Rasyonel Sayılar (ℚ)
Rasyonel sayılar, bir tam sayının başka bir tam sayıya bölümü olarak ifade edilebilen sayıları kapsar. Yani, a/b formundaki tüm sayılar, burada a ve b tam sayılar olup, b sıfırdan farklıdır. Rasyonel sayılar kümelerine örnek olarak 1/2, -3/4, 5 gibi sayılar verilebilir.
Rasyonel sayılar, ondalık veya kesirli biçimde ifade edilebilirler ve bu sayıların ondalık yazılımı ya sonlu ya da döngülü bir yapıya sahiptir. Rasyonel sayılar, reel sayılar kümesinin önemli bir alt kümesidir ve genellikle ℚ sembolü ile gösterilir.
4. İrrasyonel Sayılar
İrrasyonel sayılar, rasyonel sayıların aksine, bir kesir olarak ifade edilemeyen sayılardır. Bu sayılar, ondalık olarak yazıldığında sonsuz ve döngüsüz bir yapıya sahiptirler. İrrasyonel sayılara örnek olarak √2, π (pi), e (Euler sayısı) verilebilir.
Bu sayılar, doğada ve geometride sıklıkla karşımıza çıkar. Örneğin, bir çemberin çevresinin çapına oranı olan π irrasyonel bir sayıdır ve bu oran matematiksel hesaplamalarda çok önemli bir yere sahiptir.
5. Reel Sayılar (ℝ)
Reel sayılar, rasyonel ve irrasyonel sayıların birleşimi ile oluşan kümedir. Yani, reel sayılar, sayı doğrusundaki tüm noktaları ifade eder ve ∞’ye kadar uzanan bir bütün sayılar yelpazesini kapsar. Reel sayılar kümesi, hem sonlu hem de sonsuz bütün sayıları kapsadığı için matematiğin çok önemli bir parçasıdır ve ℝ sembolü ile gösterilir.
Reel sayılar kümesi, süreklilik özelliğine sahiptir ve bu nedenle analiz ve kalkülüs gibi matematiğin temel alanlarında kullanılır. Reel sayılar, sayı doğrusundaki her bir noktaya karşılık gelir ve bu nedenle, aritmetik ve geometrik hesaplamalarda çok önemlidir.
6. Karmaşık Sayılar (ℂ)
Karmaşık sayılar, reel sayıların da ötesine geçerek, hayali birim olarak adlandırılan ve i ile gösterilen bir bileşen içerirler. Karmaşık sayılar, a + bi formunda ifade edilir; burada a reel kısmı, b ise hayali kısmı temsil eder ve i ise √-1 olarak tanımlanır.
Karmaşık sayılar, elektrik mühendisliği, kuantum fiziği ve sinüs dalgaları gibi birçok bilimsel ve mühendislik uygulamasında kullanılır. Bu sayılar, ℂ sembolü ile gösterilir ve reel ve hayali bileşenlerin birleşimi sayesinde iki boyutlu bir düzlemde temsil edilirler. Bu düzlem, karmaşık düzlem olarak adlandırılır ve bu düzlemde her bir karmaşık sayı, bir nokta olarak ifade edilir.
Sonuç
Sayı kümeleri, matematiğin temel taşlarından biridir ve farklı sayı türlerini anlamak, matematiksel analiz ve modelleme için çok önemlidir. Doğal sayılar, en basit haliyle saymayı ve sıralamayı sağlar. Tam sayılar, negatif sayıları ve sıfırı da içererek daha geniş bir perspektif sunar. Rasyonel ve irrasyonel sayılar, kesirli ve sonsuz yapılarıyla reel sayıların temelini oluşturur. Reel sayılar ise sayı doğrusundaki tüm noktaları kapsar ve süreklilik özelliği taşır. Son olarak, karmaşık sayılar, reel ve hayali bileşenleri birleştirerek matematiğin ve bilimin daha ileri düzeydeki problemlerine çözüm sunar.
Bu farklı sayı kümeleri, matematiksel düşüncenin ve bilimsel analizlerin temellerini oluşturur ve bu nedenle her biri ayrı ayrı büyük bir öneme sahiptir.
- Site İçi Yorumlar













Yorum Yaz